19. Correct. The answer is false. In order to calculate the probability that
well A2 contained commercial reserves, we have to employ the Bayes's rule. The essence of the Bayesian approach is to provide
a mathematical rule explaining how you should change your existing beliefs in
the light of new evidence. In other words, it allows statistician to combine
new data with their existing knowledge or expertise.
In the context of the wildcat exploration, we
can think about Bayes' rule in terms of updating the
belief that well A2 contains commercial reserves in the light of the
confirmation of the existence of profitable reserves (event B). Specifically,
our posterior belief P(A|B) is calculated by multiplying our prior belief P(A)
by the likelihood P(B|A) that B will occur if A is true:
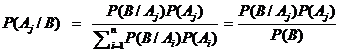
The power of Bayes'
rule is that in many situations where we want to compute P(A|B)
it turns out that it is difficult to do so directly, yet we might have direct
information about P(B|A). Bayes' rule enables us to
compute P(A|B) in terms of P(B|A).
We know P(B) = 0.19 from question 18. Applying
the Bayes’ rule, we can calculate the probability
that profitable reserves come from well A2:
P(A2 | B) = (0.25*0.3) / 0.19 = 39.47%