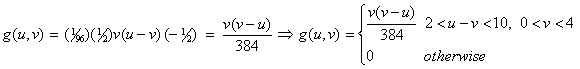11. Correct. The
answer is false. It is possible to obtain such a formula by making a change
of variable: u = x + 2y and v = x.
The simultaneous solution is x = v
and y = 1/2(u - v). Thus, after
changing variables, the integration region changes from 0 < x < 4 and 1 < y < 5 (region E),
changes to 0 < v < 4 and 2 <
u - v < 10 (region D), which is shown shaded in the
following figure:

We have to apply Theorem 2-4,
p.45 in Schaum's Outlines Probability and Statistics. Let x and y be continuous random
variables having joint density function f(x,y,).
Let us define
u = φ1(x, y), v = φ2(x, y) where x = ψ1(u, v), y = ψ2(u, v). The joint density function of u
and v is given by g(u, v) where:
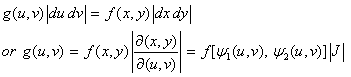
where J = Jacobian determinant (or simply Jacobian) that is given by:
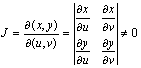 .
.
The determinant of 2x2 matrix
![]()
![]()
is equal to: ad - cb. In the problem, the Jacobian is:
So, the change of variable allows us to obtain: