Self Test 3 for Probability
and Statistics
Mathematical Expectation
This test was constructed by Dr. Carol Dahl and Arturo Vasquez based on the Schaum's Outline Theory and Problems of Probability and Statistics by Murray R. Spiegel. If you need more review refer also to this outline.
Expectation of Random Variables, Functions of Random Variables, and some Theorems
1. True False. A financial economist is analyzing the return of a certain asset in a mineral commodity market. He realized that the expected return of the mineral asset in one year depends on a discrete random variable Z whose probability function is given by f(z) = (1/2)z (where z= 1, 2, 3, . . . ). After one year, the expected return of the investment is one ($ ten thousands) (Contributed by Zauresh Atakhanova and Arturo Vasquez).
2. True False. A petroleum engineer has built a mathematical model to analyze the behavior of a certain oil well. The oil production (in thousand barrels) is considered as a continuous random variable Y which has the following probability density function:
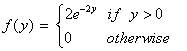
According to this model, E(Y) = 500 barrels, E(Y2) = 1/2.
3. True False. The number of failures of a certain oil pipeline during a period of five years is represented by a random variable X which has the following density function:

A mechanical engineer has determined that the number of oil spills (Y) depends of X according to the following function: Y = 2X + 10. The probability of having between 12 oil spills and 16 oil spills in five years is 30%. The expected number of oil spillsis 10. (Contributed by Arturo Vasquez).
4. True False. A crazy investor wants to risk some money by investing in an asset whose value depends on the copper price. Let X a random variable which represents the possible values of the copper price in one year. According to some mineral economists who are advising the crazy investor, the copper price can achieve six possible values during the year (100 $ per ton): {1, 2, 3, 4, 5, 6}. The probability of each event is the same. Hence, P(x) = 1/6. If the mineral economists believe that the value of the asset (Y) depends on the copper price by means of the following function: Y = 2X2 - 5, what is the expected value of the asset after one year? The value is approximately US$ 2,500 (contributed by Arturo Vasquez).
5. True
False. A mining company has two ore deposits which contain copper and zinc.
Let X the quantity of copper which is
recoverable from the first deposit and Y
the quantity of zinc that can recovered from second deposit (both quantities
are expressed in thousands tons) . Both variables are random because the
company's mining engineers don't exactly know the amount of each mineral in the
deposit. However, they know the joint density function of both variables:

What is the expected quantity of copper and zinc that is recoverable? If the area of the deposit of copper is expanded 3 times and the area of the deposit of zinc is expanded 2 times due to a success in the mining activities in the zone, the engineers consider that the production of copper and zinc can increase by the same proportions: 3X and 2Y. What is the expected total quantity of mineral (the sum of the random variables with the new coefficients) which is recoverable from the mine site? The expected values of copper and zinc are 2,667 tons and 3,444 tons respectively. The expected total quantity of mineral after the expansion is 15,667 tons (Contributed by Arturo Vasquez).
Variance, Standard Deviation and Some Theorems on Variance
6. True
False. Two different machines in a factory are able to produce
from 1 ton to 6 tons of refined steel plates individually. The steel is made
and packaged in lots of 1 ton each to be shipped to the factory's customers. It
has been shown through a number of studies that the output of each machine
varies day to day randomly and that the performance of one machine is
independent of the other. The probability of any given output is equal each
day. (There is a 1 in 6 chance that there will be 1 ton of output, or 2 tons of
output, or . . . , or 6 tons of output). The variance (a) and the standard
deviation (b) of the total number of tons produced per day by both machines
are:
a. 91/6
b. (91/6)1/2
(Contributed by Dustin Menger)
7. True False. The set {23.73, 24.46, 24.29, 19.64, 17.65, and 17.53} represents OPEC ref. basket oil prices of the second semester of 2001. (a) The first moment about the origin is 21.22 and (b) the second moment about the mean is equal to 9.18 (Contributed by Maria Sanchez).
8. True False. In Problem 2, we had a petroleum engineer who was analyzing the behavior of a certain well. Now, the company which hired the engineer wants to know the variance and the standard deviation of the oil production of the well. The variance (a) and the standard deviation (b) for the random variable from Problem 2 are: (a) 1/4 and (b) 1/2.
Standardized Random Variables
9. True False.
A mineral economist is analyzing a sample of ten observations of the cooper
price in the
Average U.S. Produce Cooper Price (cents per pound)
![]()
Source:
He wants to standardize the copper price in order to compare its evolution with that of other mineral prices in the last years so as to verify if there were certain regularities or co-movements among prices. The standardized series is:
![]()
(Contributed by Arturo Vasquez)
Moments and Moment Generating Function
10. True False. An oil company has developed a smart model which describes the probability of extracting certain quantities of oil (X) in a well (barrels per day). The density function of this model is:

X is expressed in thousands of barrels per day. It is necessary to calculate the mean and standard deviation of oil production because the managers of the company want to know if the expected production satisfies the requirement of 1500 barrels per day, which is the production level to break even. The chief statistician suggests using a moment generating function to determine the mean and standard deviation. Using this approach, the expected production level is 1600 barrels per day and its standard deviation is 500 barrels per day. It is profitable to exploit the oil well (Contributed by Arturo Vasquez).
Variance for Joint
Distribution, Covariance, and Correlation
11. True False. A senior mining engineer is analyzing the presence of copper (main mineral) and silver (by-product) in a certain geological formation. The amounts of copper and silver are random variables U and V respectively. The joint probability function of the U and V (in thousand of tons) is given by f(u,v) = b(2u+v), where u and v can assume all integers such that 0 ≤ u ≤ 2 and 0 ≤ v ≤ 3, and f(u,v) = 0 otherwise. The engineer computes the following statistic parameters in order to report this information to the management of the mine site where he is working:
(a) E(U) = 29/21
(b) E(V) =13/7
(c) E(UV) = 17/7
(d) E(U2)= 17/7
(e) E(V2) = 32/7
(f) Var (U) = 230/441
(g) Var (V) = 55/49
(h) Cov(U,V) = -20/147
(i) r= -0.2103 (correlation coefficient)
(Contributed by Dustin Menger and Arturo Vasquez)
12. True False. There are two mineral assets (X and Y) which returns (in US$) are negatively associated along time. An investor is thinking about buying both assets in order to diversify his portafolio, but he firstly wants to know the variability of the sum of the two assets before buying them. If the mineral stock market reports that the variance of X is 50, the variance of Y is 20, and the covariance of X and Y is -27, the standard deviation is US$ 10. (Contributed by Arturo Vasquez).
Conditional Expectation, Variance and Moments
13. True False. In problem 10, a senior mining engineer was working with a joint probability function of two discrete random variables U and V (amounts of cooper and silver respectively). The probability function is given by f(u,v) = b(2u+v), where u and v can assume all integers such that 0 ≤ u ≤ 2 and 0 ≤ v ≤ 3, and f(u,v) = 0 otherwise. The conditional expectation of V given U=2 is E(V|U=2)=20/11. (Contributed by Dustin Menger)
14. True False. A mineral mining operation faces the following probabilities of finding copper (Cu) and/or molybdenum (Mo) in the stated quantities:
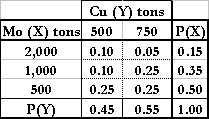
The expected value of copper given that 2,000 tons of molybdenum has been discovered is 583.33 tons. The conditional standard deviation of molybdenum given that 750 tons of copper has been discovered is 431 tons (Contributed by Sara Russell).
Chebyshev's
Inequality and Law of Large Numbers
15. True False. In an African country, a petroleum engineer is working with a mineral economist in determining how many barrels a small oil well can produce. Let X a random variable which represents the oil production. The engineer determined that the well can produce an average of 33 barrels with a variance of 16. However, the management of the oil company considers that a well should produce between 23 and 43 so as to obtain profits. The mineral economist has received the task to determine the probability that the oil well produces between the expected minimum and maximum values required by the management. After carrying out the analysis, the mineral economist determine that at least the well will produce in this range with a probability of 21/25 = 84% (Contributed by Arturo Vasquez).
16. True False. A mineral economist has in a database a sequence of different mental prices P1, P2, P3, . . . If these prices are independent and identically distributed and if these prices has a common mean and variance: E(Pi) = μ and Var(Pi) = σ2. What is the value of the average of these prices? To what value does the average price converge? The problem has no solution because we have prices with different probability distribution functions. The sum of these prices doesn't have a known distribution, for it is impossible to determine the average and its value of convergence (Contributed by Arturo Vasquez).
Other Measures of Central Tendency and Percentiles
17. True False. The density function of a continuous random variable Z, which represents the population's income of a mineral country, is:
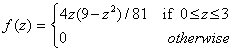
Z is expressed in thousand US$ dollars. (a) The mode is 1.73, (b) the median is 1.62, and (c) the comparison between the mode, median and mean is Mean<Median<Mode (Contributed by Dustin Menger).
18. True
False. In problem 16, we had the density function of the population's income of
a mineral country. What is the income of the first 10% of the population, the
25% of the population, and the 75% of the population? The values are: US$ 500,
US$ 1200, and US$ 2121 (Contributed by Arturo Vasquez).
Other Measures of Dispersion
19. True False.
In problem 16, we had the density
function of the population's income of a mineral country. The
Moments, Skewness and Kurtosis
20. True
False. The returns of a mineral asset and their probabilities are given in the
following table:
|
Returns |
2 |
4 |
6 |
8 |
|
Probabilities |
0.4 |
0.3 |
0.2 |
0.1 |
In order to make an investment decision about this asset is necessary to
know some important information about the probability distribution. The
distribution is symmetric and the returns tend to share the same frequency of
occurrence (Contributed by Arturo Vasquez).