Self Test 4 for Probability
and Statistics
Special Probability Distributions
This test was constructed by Dr. Carol Dahl and Arturo Vasquez based on the Schaum's Outline Theory and Problems of Probability and Statistics by Murray R. Spiegel. If you need more review refer also to this outline.
The Binomial Distribution
1. True False. If 10% of the wells drilled by an oil company in a field contain natural gas, the probability that out of 4 wells drilled at random
(a) 1 will be defective is 29.16%
(b) less than 2 nails will be defective is 94.77%
2. True
False. The probability that a sizable amount of raw diamonds (0.5% of the weight
of a rock load) will be extracted from a given ore load from a certain diamond
mine in
a.
9 will
have a sizable content of raw diamonds is 4.031%
b.
all ten
will have a sizable content of raw diamonds is 0.6047%
c.
greater
than 8 loads will have a sizable diamond content is 4.6357%
The Normal Distribution
3. True
False. The number of ore diggers who are necessary for burrowing a mineshaft
follows a normal distribution with mean 20 and variance 25, N(20,25). The probability
that the number of diggers is between the mean and 24 is 0.523.
4. True False. A fuel for a certain airplane is going to content a percentage (called X) of a particular additive. The specifications require that X is between 30 and 35 percent. The refinery, which produces that fuel, will obtain a net profit according to the following function of X:
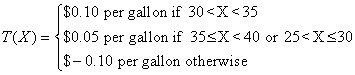
If X follows a normal distribution with mean 33 and standard deviation of 9, the expected profit E[T] 6.74 cents per gallon (Contributed by Arturo Vasquez).
5. True
False. In the north of
6. True False. The mean weight of 600 male employees at a certain oil company is 151 lb and the standard deviation is 15 lb. Assuming that the weights are normally distributed, the number of employees that weigh (a) between 120 and 155 lb is 360, (b) the number of employees that weight more than 185 lb is 6 (Contributed by Claudio Valencia).
7. True
False. A study indicated that the copper mines in
The Poisson
Distribution
8. True
False. Ten percent of the bulldozers used in a mine site tend to fail. Find the
probability that in a sample of 10 bulldozers chosen at random exactly two
fail. The probability is 0.15 (Contributed by Arturo Vasquez).
9. True False. The average number of cars that randomly arrives to a gas station is 24 per hour. The probability that 5 cars arrive in a period of 12 minutes is 20% (Contributed by Arturo Vasquez).
Central Limit Theorem
10. True False. A multinational mining company expects to receive an average of 50 environmental claims made by the regulatory agencies of the countries where it operates. The actual number of claims is a random variable and it is well described by a Poisson distribution. The value of each environmental claim is a random variable, independent of all other claims, with a mean of $500,000 and a standard deviation of $100,000. a) The probability of having 60 claims is 4.21% b) If the company actually has 55 claims, the probability that the total value of those claims will be more than $29,000,000 is 2.17% (Contributed by Arturo Vasquez).
11. True False. A group of excavator machines in a copper mine can extract ore loads that have an average weight of 300 tons and a standard deviation of 50 tons. The probability that 25 ore loads taken at random can exceed the capacity of an ore processing facility which can process 8,200 tons is 2% (Contributed by Arturo Vasquez).
Multinomial and
Hypergeometric Distributions
12. True False. The Peruvian Tax Administration is auditing the income tax returns of several mining companies because it suspects that some of these companies didn't fill their tax forms correctly (they probably didn't consider the windfalls earned after a mineral price boom which occurred last year). The probability that a tax return was properly filled out is 60%. The probability that a tax return has an error which favors the taxpayer is 20%, the probability of having a tax return with errors which favors the government is 10%, and the probability of having a tax return with both errors is 10%. The General Tax Controller chooses ten tax returns at random. The probability that 5 tax returns were properly filled out, 3 have errors which favor the taxpayers, 1 has errors which favor the government, and 1 has both kinds of errors is 5% (Contributed by Arturo Vasquez).
13. True
False. A geologist is analyzing a sample of 11 rocks of
which five content lead and six content copper. The geologist wants to choose
four rocks at random without replacement. The probability of choosing at random
exactly 3 rocks with copper is 30.30%. The expected number of rocks with copper
that can be extracted is 24/11 ≈ 2 (Contributed by Arturo Vasquez).
The Uniform Distribution
14. True False. The trucks that carry ores in a certain mine site have to pass by a certain control point each 8 minutes. A supervisor can unexpectedly arrive to the control point to verify the transportation of the valuable ore. If X is the random variable which represents the time that the supervisor has to wait until a truck passes by the control point, a) the probability that the supervisor waits for a truck less than 5 minutes is 1/8 b) Thye probability that the supervisor waits for a truck more than two minutes is 1/4. (Contributed by Arturo Vasquez).
15. True False. The mean (a) and the variance (b) of the uniform density, which is defined by
f(x) = (b-a)-1, a ≤ x ≤ b;
= 0, otherwise.
Are:
(a) m =1/2(a+b)
(b) (b) s2= (b-a)2/12.
(Contributed by Joe Mazumdar)
The Chi-Square Distribution and its relation with the Normal Distribution
16. True False. The graph of the chi-square distribution with 5 degrees of freedom is shown in the figure below. The values χ 21 and χ21 for which
(a) the area to the right of χ22 = 0.05,
(b) the total area to the left of χ21 and to the right of χ22 = 0.05,
(c) the area to the left of χ21 = 0.10,
(d) the area to the right of χ22 = 0.01.
Are:
(a) 11.1
(b) 0.831 and 12.8
(c) 1.61
(d) 15.1
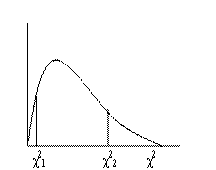
(Contributed by Joe Mazumdar)
17. True False. A petroleum engineer is modeling the number of wells with oil in a certain field by using a statistical model. He realized that the number of wells with oil 'X' in the field follows a normal distribution with mean 7 and variance 4. Besides, the number of wells with water is defined by the following random variable: (X - 7)2. What is probability of having between 15 and 20 wells with water in the oil field? The probability is 4% (Contributed by Arturo Vasquez).
Student's t Distribution and its relation with the Normal Distribution
18. True False. The graph of Student's t distribution with 9 degrees of freedom is shown in the figure above. The value of t1 for which
(a) the area to the right of t1 = 0.05.
(b) the area to the left of -t1 and to the right of t1 = 0.05
(c) the area between -t1 and t1 is 0.99
(d) the area to the left of -t1 is 0.01
(e) the area to the left of t1 is 0.90.
Are:
(a) 1.83
(b) 2.26
(c) 3.25
(d) -2.82
(e) 1.38
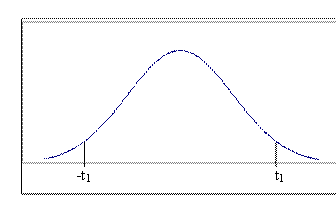
(Contributed by Joe Mazumdar)
19. True False. Two mechanical engineers are evaluating the relation between the diameter and thickness in a sample of pipelines in order to analyze the probability of having a leakage. They realize that the diameter 'D' follows a normal distribution with a mean of 2 meters and a standard deviation of 0.5 meters, and the thickness 'K' follows a Chi-square distribution with a mean of 20 inches. It is known that the probability of having a leakage depends on a variable defined by the ratio 'L' of the standardized diameter and the square root of the thickness divided by its mean. What is distribution function to model the probability of having a leakage? The distribution function is unknown (Contributed by Arturo Vasquez)
The F Distribution
20. True False. Using the table for the F distribution, the values of (a) F0.99, 15, 9, (b) F0.01, 15, 9, (c) F0.95, 10, 15, (d) F0.05, 8, 30.
Are:
(a) 4.96
(b) 0.257
(c) 2.54
(d) 0.325
(Contributed by Joe Mazumdar)