7. Correct. The answer is true

Let Chile = country A and Australia = country B then

m_A = 15 years, m_B = 7 years

s_A = 5 years, s_B = 2 years

n_A = 10, n_B = 10

X_A - X_B = 8 years

Difference in means is given by;

m_A-B = 15 - 7 = 8 years

Difference in standard deviation is given by

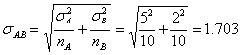
Standardized variable for the difference in the means is given by;

Z = [(X_A - X_B) - (m_A - m_B)] / s_A-B

Z = [10-8] / 1.703 = 1.17

Required probability = (area under normal curve to the right of Z = 1.17)

= 0.5 - 0.3790 = 0.121

Therefore, the probability that the Chilean copper mines have a mean lifetime at least 10 years greater than that of their Australian counterparts is 0.121.