13. Correct. The answer is true. Let X be a random variable which represent the
number of rocks with copper extracted at random. Let N be the number total
number of rocks in the sample. M is the number of rocks with copper. N - M is
the number of rock with lead. “n” is the sample taken
at random
N = 11, M = 6, N - M = 11 - 6 = 5, n = 4.
The scenario satisfies the requirements of a hypergeometric experiment, for the probability distribution
function of X is:
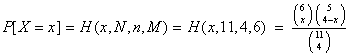
The expected value of this distribution is: E[X] = n[M/N]
The requested probability is P[X=3] = ![]() ≈ 30.30%.
≈ 30.30%.
The expected value is E[X] = 4*(6/11) = 24/11 = 2.18 ≈ 2.