19. Correct. The answer is false. There is an important theorem in Statistics which links the normal, the Chi-square, and the t-student distribution function which establishes that the ratio of a random variable 'Z' which has a standardized normal distribution and the square root of another random variable 'Y' which has a Chi-square distribution with 'r' degrees of freedom follows a t-student distribution function with 'r' degrees of freedom, provided that Z and Y are independent.
![]()
In our case, the standardized diameter is Ds = (D - 2)/0.5 ~ N(0,1), and K ~ χ2(20) because the mean of the thickness is equal to the number of degree of freedom of the Chi-square distribution. Therefore, we can define 'L' as follows:
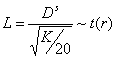
'L' follows a t-student distribution with 20 degrees of freedom.