Uncertainty is a predominant characteristic of
the modern world. Quantifying uncertainty and making inferences from a
bewildering array of data are increasingly valuable skills in the current
world. Probability and Statistics are foundation tools needed for these skills
and are prerequisites for our Mineral Economics Program. The following self
test is designed to help you review the concepts that will be important to know
for courses that deal with uncertainty or estimating statistical relationship.
Self
Test 1 for Probability and Statistics
This test, constructed
by Zauresh Atakhanova,
Carol Dahl, and Arturo Vasquez has a mineral/energy slant and supplements the
material in Schaum's Outline Theory and Problems
of Probability and Statistics by Murray R. Spiegel. If you need more review
refer to Schaum's outline.
Sets
and Probability
Sets
Sets, which are collections of objects, are at the foundation of
Probability and Statistics. The 38 elements in groups 3 through 12 of
the periodic table below are called 'transition metals.' As with all metals,
the transition elements are ductile and malleable and they conduct electricity
and heat. Their valence electrons are present in more than one shell. This is
why they often exhibit several common oxidation states. The atomic mass or
weight of an element is its average number of protons plus neutrons and the
atomic number, listed in the left upper corner in the periodic chart below, is
its number of protons (contributed by Carol Dahl).
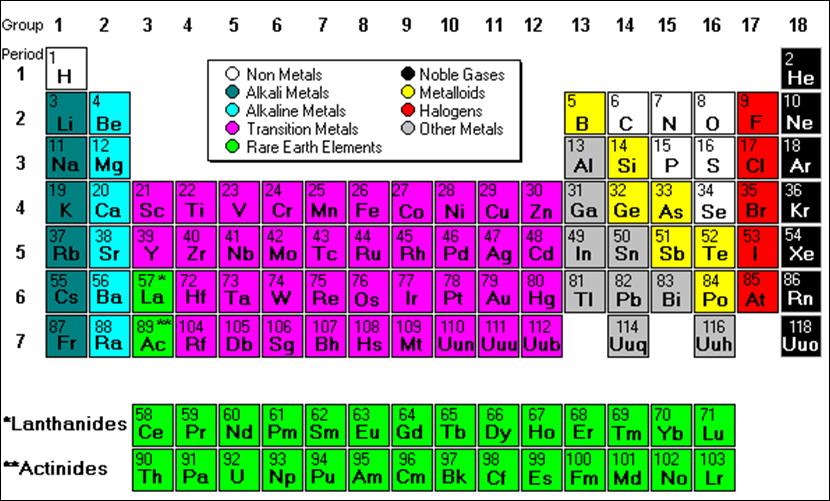
1. True False. We can describe the set 'T' for the transition
metals by the property method using
atomic numbers 'x'. So, we have T = { x: (21≤ x ≤ 30) or (39≤
x ≤48) or (72≤x ≤80) or (104≤x ≤112)}.
2. True False. Let the set T above, which is the
transitional metals collection, be the universal set. Let A = {Gold (Au),
Silver (Ag), Copper (Cu) } and B = {x | 26 < x < 30}. Where
x again is the atomic number of the element. Then, A U B = {either A or B (or
both)} = {Fe, Co, Ni, Cu, Zn, Au, Ag}
3. True
False. Again let A = { Au, Ag, Cu} and B = { Fe, Co, Ni, Cu, Zn}. Then, A ∩
B = {elements in both A and B) = Cu}.
4. True False. Again let T, the transitional metals, be the
universal set, A = {Au, Ag, Cu} and B = { Fe, Co, Ni, Cu, Zn}. Then, A ∩ B' = {All transition
elements but Gold or Silver}
5. True False. Again let T, the transitional metals, be the
universal set, A = {Au, Ag, Cu} and B = { Fe, Co, Ni, Cu, Zn}. A'UB' =
{Anything but Copper}
6. True False. Again let T, the transitional metals, be the
universal set, A = {Au, Ag, Cu} and B = { Fe, Co, Ni, Cu, Zn}. Then, B - A =
{Fe, Co, Ni, Zn}.
7. True False. Again let T, the transitional metals, be the
universal set, A = {Au, Ag, Cu} and B = { Fe, Co, Ni, Cu, Zn}. Then, A' - B' =
{any element with atomic number between 26 and 30}
8. True False. Again let T, the transitional metals, be the
universal set, A = {Au, Ag, Cu} and B = { Fe, Co, Ni, Cu, Zn}. Then (A ∩
B) U (A ∩ B') = {A}.
Random
Experiments, Sample Spaces and Events
9. True False. Random variables are sets with probabilities
attached to them. Let A be a set containing five metal samples of a certain polymetallic
mine: A = {18k Gold (Au1), 14k Gold (Au2), Silver (Ag),
Copper (Cu), Aluminum (Al)}. Suppose you draw a metal at random from set A with replacement. Each sample is equally
likely to be drawn. The probability that you draw gold on the first draw is
2/5.
10. True False. In the last exercise, we worked with set A
containing five metal samples. Suppose that 14k Gold sample was contaminated
and you threw it away. So, your set is now A - Au2 = {Au1,
Ag, Cu, Al}. You draw one sample with replacement at random to assay. The
probability that you draw Gold or Silver is 1/4.
11. True
False. A Petroleum Engineer is analyzing a set of oil samples from different
new oil fields in the Middle East in order of study their properties for
commercial purposes. She received 15 samples: S = {crude oil with 'x' equal
distinct integer values of API degrees | 20o < x ≤ 35o).
In the roster method S = {21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35}. In this set, heavy oils are considered to have an API degree between
21 and 24 and light oils to have an API degree between 31 and 35. The engineer
has to show a report to the production manager of an oil company tomorrow
morning. So, she needs to select a random sample without replacement of 3 crude
oils so as to prepare this report as soon as possible. The probability that
engineer selects light crude oils in the three draws is
about 2.20% (contributed by Arturo Vasquez).
12. True
False. In exercise 11, the probability that the engineer draws heavy oil in the
first and second draws is (4/15)*(4/15).
13. True
False. The company 'Quick Oil' has recently discovered two gas reservoirs with
a high content of natural gas liquids. The reservoir A contains: A = {propane,
butane, ethane, water}. The reservoir B probably contains: B = {heptane,
hexane, octane, water}. The probability of producing Liquefied Petroleum Gas
(LPG), which is propane and butane, from reservoir A is equal to 5%, whereas
that the probability of producing LPG from reservoir B is equal to 90%
(contributed by Arturo Vasquez).
Calculation of Probabilities
14. True False. A human resource company is looking for a mechanical engineer
specialized in pipeline welding to help build a gas pipeline in Peru's jungle.
In its database the company has a set of 52 engineers: 13 engineers from U.S.A,
13 from U.K, 13 from Russia and 13 from India. The years of experience for each
country's professionals has a uniform distribution from 1 to 13 years with
experience rounded to the closest year. Thus each country has an engineer with
1 year of experience, 2 years, . . . 13 years of experience. In a first step of
the selection process, the company will select engineers at random. The
probability of drawing an engineer with exactly ten years' experience or an
engineer from Russia is 4/13.
15. True False. In exercise 14, the probability of drawing
neither an engineer with 4 years' experience nor an engineer from India is
10/13.
Conditional Probability and Independent Events
16. True
False. A mineral engineer is working with ore samples to identity their
quality. The engineer organizes the ores in a set by the predominant minerals
in each ore: M = {gold1, gold2, gold3, silver1, silver2, silver3, zinc1, zinc2,
zinc3, copper1, copper2, copper3, tin1, tin2, tin3, lead1, lead2, lead3}. The
number '1' represents a high-quality mineral, the number '2' represents a
middle-quality mineral, and 3 represents a low-quality mineral. The precious
metals are gold and silver, whereas the other elements are non- precious metal.
The engineer conducts two draws without replacement. The probability of
selecting a low-quality gold ore in the first draw and of selecting a non-precious
ore in the second draw is 1/17 ≈ 0.059 or 5.9% (Contributed by Arturo
Vasquez).
17. True False. In exercise 16, if
the drawing process is conducted with replacement, the probability of selecting
a silver ore in the first draw (event A), a zinc ore in the second draw (event
2), and a copper ore in the third draw (event 3) is 1/216.
Total Probability and Bayes' Rule
18. True False. A wildcat oil firm is exploring in a certain area of the Peruvian Amazon
in order to confirm the existence of crude oil reserves. The wildcat is
analyzing a statistical study about exploratory operations from another company
which was looking for hydrocarbons in the same area years ago. A geologist of
the wildcat found some probabilistic information in the form of a tree diagram.
This information is about the probability of discovering oil in the area. There
are three exploratory wells in the area: A1, A2, and A3.
The probability of finding oil in these wells is shown in the tree diagram
(drilling stage). However, there are certain probabilities that each well has
commercial reserves. This information is determined by economic studies. The
event of having commercial reserves 'after' discovering oil in a well is
denominated 'B' in the tree diagram.
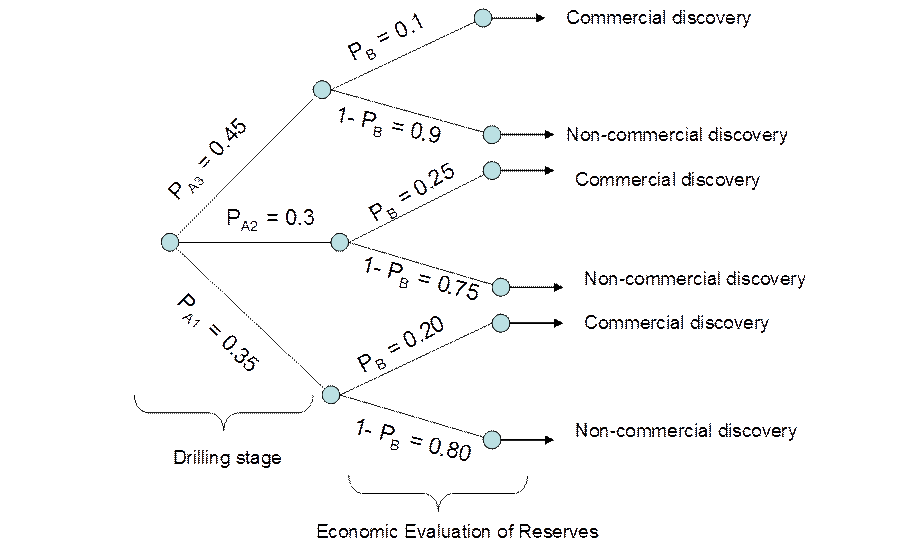
The probability of having a commercial discovery of oil reserves in the
area 21%. (Contributed by Arturo Vasquez).
19. True False. In exercise 18, we've calculated the probability of discovering
commercial reserves. Because the probability of finding profitable reserves are
not negligible for the exploration standards, the wildcatter initiates the
exploration works. After drilling a lot in the area, the wildcat discovered
commercial reserves. The probability that profitable reserves come from well A2
is 30%.
20. True
False. This is an example of petroleum exploration using Bayesian analysis. In
a certain area of Nigeria, which has a huge sedimentary deposit, seismic
studies in the area found out the existence of two zones E1 and E2 which contain
certain anomalies. Geologists have determined two probable states of nature: a)
E1 could have 7 anomalies that contain no oil and 5 anomalies that contain oil,
and b) E2 could have 9 anomalies that contain no oil and 3 anomalies that
contain oil. They determines the following probabilities for those events:
P(E1) = 0.33, whereas P(E2) = 0.67. A wildcatter drilled on one of the seismic
anomalies and realized that the well is a dry hole, which we call event 'B'.
This new information will help the wildcatter to revise original estimates of
each of the hypothesized state of nature. The probability that the first
anomaly drilled will be dry if in fact E1 is the true state of nature
P(E1|B)=0.52. The probability that the first anomaly drilled will be dry if in
fact E2 is the true state of nature P(E2/B) = 0.46 (contributed by Mansoor Al-Harthy and reviewed by
Carol Dahl and Arturo Vasquez).
Probability
Using Combinatorial Analysis
21. True False. A mineral laboratory is analyzing 8 samples of copper, 3 samples of zinc, and 9 samples of aluminum. If 3 samples are drawn at random without replacement, the probability that 2 are copper and 1 is zinc equals 7/ 95.
22. True
False. Out of 7 senior mining companies and 6 junior mining companies, a
committee of 4 senior mining companies and 2 junior mining companies is to be
formed. If any of the mining companies can be included, the number of possible
committees is 525 (contributed by Claudio Valencia).
23. True
False. A technical supervisor of an energy regulatory agency in certain
developing country is checking the construction of an oil pipeline in the
highlands. Specifically, he is looking for failures in the pipeline's welding.
He can find 6 possible events after checking the X-ray shots of each pipeline
junction: excellent welding (A), very good welding (B), good welding, (C) small
porosities in the welding (D), large porosities in the welding (E), and a
non-welded junction (F). If the probability of finding D is 1/6 and the
probability of finding not D is 5/6 then the probability that event (D) occurs
in 3 inspections of 5 if the events are mutually exclusive is 2.9% (contributed
by Arturo Vasquez).