Self Test 2 for Probability and Statistics
Random Variable and Probability
Distributions
This test was constructed by Zauresh Atakanova, Carol Dahl and Arturo Vasquez Cordano based on the Schaum's Outline Probability and Statistics by Murray R. Spiegel. If you need more review refer also to this outline.
Discrete Random Variables and Cumulative Probability Distributions
1. True False. A mineral engineer is studying two 'fair' mineral sample sets in order to know their grade. He designed a quality classification which assigns number from 1 to 6. '1' means an ore with the lowest grade level and '6' means an ore with the highest quality level. In each mineral set there are 6 kinds of ore which grades go from 1 to 6. So, he has twelve ore in total. Suppose the mineral engineer conducts an experiment where he selects one sample of the first mineral set and one sample of the other mineral set and let the random variable X denote the sum of the grade points that he previously defined. What is the probability function of the engineer's random variable? The probability function for X is:
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
f(x) |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
(contributed by Arturo Vasquez and Zauresh Atakhanova)
2. True False. The cumulative distribution function F(x) for the random variable X of problem 1 is F(x) = 36
3.True False. A smart geologist has made a probabilistic model of discovering crude oil in a certain field of the Brazilean Amazonia. Let 'x' be the random variable (number of barrels of probable reserves), which has the following density function:
f(x) = ax(1-x) if 0 < x < 1 and 0 otherwise
He realized that the domain of this functions goes from 0 to 1 billion barrels of probable reserves. What is the value of 'a' in this smart formula? The value is 5 (contributed by Arturo Vasquez).
4.True False. In the last exercise, we obtained the coefficient 'a' of the oil discovery function. The probability of discovering 0.5 billion barrels of probable reserves is 45%.
5. True False. A mechanical engineer is testing some segments of a pipeline is order to verify if there are some fissures. He defines a continuous random varible: number of fissures per segment 'x'. He realizes that the cumulative probability function of finding fissures is:
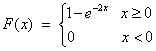
The engineer is interest in knowing: a) the form of the density function, b) the probability of having more than 2 fissures in a pipeline's segment, c) the probability of finding out 2-4 fissures in a pipeline's segment. A statistician performs the computation and answers: a) 2e-2x (x>0) and 0 (otherwise), b) 1.83%, c) 1.79% (contributed by Arturo Vasquez).
Joint Distributions and Independent Variables
6. True False. A
team conformed by a mining engineer and a mineral economist have designed a
probabilistic model to infer the probability of discovering probable reserves
of copper in a centain grassroots area of
7. True False. The marginal probability functions of (a) U and (b) V for the random variables from problem 6 are: a) P(U = u) = 1/7, 1/3, and 11/21, b) P(V = v) = 1/7, 3/14, 2/7, and 5/14 (contributed by Zauresh Atakhanova).
8. True False. A mining company has designed a statistical model which calculates the probability of finding high-grade ore in a certain mine site in the Peruvian highlands. The joint density function depends on two stochastic variables: x is amount invested in operating the mine site per year (millions of dollars), y is number of millions of tons (new reserves). The density function is:
![]()
It is necessary to compute the parameter 'c' in order to complete the model. The company's management wants to know what probability gives the model if it is invested between $ 1 and $ 2 millions of dollars in operating the minesite, as well as it is requested 2 to 3 billions tons of reserves. The answer is: a) c = 1/46, b) 2.37% (contributed by Carol Dahl and Arturo Vasquez).
9. True False. From problem 8 we know that the joint density function is f(x,y) = cxy (0 < x < 4, 1 < y < 5) and 0 (otherwise). Do you consider that the amount investmented in operating the mine site and the number of reserves are independent events? The answer is 'yes'
Change of Variables
10. True False. A mechanical engineer is evaluating
the security system of an oil pipeline in
f(x) = 2-x x = 1, 2, 3, . . .
f(x) = 0 otherwise.
Besides, the engineer found out that the probability of having an oil spill (y) after a failure depends on the random variable x such that y = x4 + 1. Therefore, it is possible to show that the probability function for the random variable y is:
g(y) = 2-(y-1)^(1/4) y =
2, 17, 82, . . .
g(y) = 0
otherwise
(contributed by Carol Dahl and Arturo Vasquez).
11. True False. From problem 8, we know that the joint density function of the probability of discovering of high-grade ore is f(x,y) = cxy (0 < x < 4, 1 < y < 5) and 0 (otherwise). According to an environmental engineer, it is also possible to determine the probability of affecting an underground river located near the minesite. That river helps maintain the level of the superficial water in the area where many native communities live. The company needs to know this information since the Peruvian Mining Supervisory Agency might impose an environmental fine if this river was affected. The engineer proposes a model that depends on the random variable u = pollution level, which in turn depends on x and y according to the formula: u = x + 2y. What is the probability density function of u? The answer is: it is impossible to deduce this formula because both x and y are not independent events (contributed by Arturo Vasquez).
Conditional Distributions
12. True False. For the distribution of Problem 6, it is possible to deduce the following conditional distributions: a) f(v|2) = (4+v)/42, P(V=1|U=2)=5/42.
13. True False. A mining company has designed a statistical model to predict the probability of discovering zing in a certain minesite. Let x the amount invested in exploratory activities ($ million) and let y the number of reserves discovered (millions of tons). The joint density function of both random variables is:
![]()
What is the model which allows us to know the probability of discovering new reserves given that certain amount of money was invested in exploratory activities? The answer is: 2y/x2 for 0 ≤ y < 1 and 0 for other values of y (contributed by Arturo Vasquez).
Convolutions
14. True False. An energy economist who work at a stock change has been working in making a model to predict the probability that 2 oil future contracts achieve certain market value (x = value of the first oil future contract, and y = value of the second oil future contract). The density functions are:
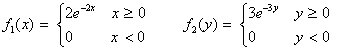
It is known that the values of x and y are independent. The analyst is considers to conform a small portafolio with these two assets. What would be the density function of the portafolio u = x + y? The answer is f1 * f2 = 6e-2x-3y (contributed by Carol Dahl and Arturo Vasquez).