Self Test for Probability and Statistics

Self Test 5 for Probability and Statistics

Sampling Theory

This test was constructed by Zauresh Atakhanova based on the Schaum's Outline Theory and Problems of Probability and Statistics by Murray R. Spiegel. If you need more review refer also to this outline.

1. True False A population consists of the four numbers 2,3,6,9. Consider all possible samples of size two which can be drawn with replacement from this population. Find (a) the mean of the population, (b) the standard deviation of the population, (c) the mean of the sampling distribution of means, (d) the standard deviation of the sampling distribution of means, i.e. the standard error of the means.

a) 5

b) 5.48

c) 5

d) 2.74

2.True False. Assume that the heights of 3500 female students at a university are normally distributed with mean 67.0 inches and standard deviation of 3.0 inches. If 80 samples consisting of 25 students are obtained, the expected mean and standard deviation of the resulting sampling distribution of means if sampling were done with replacement are 67.0 and 0.6, respectively

3.True False. In 73 samples from Problem 2 you would expect to find the mean (a) between 65.8 and 67.3 inches, and in 10 samples you would expect to find the mean less than 65.4 inches.

4.True False. The electric bulbs of brand A have a mean lifetime of 1500 hours with a standard deviation of 200 hours, while those of brand B have a mean lifetime of 1300 hours with a standard deviation of 100 hours. If random samples of 125 bulbs of each brand are tested, the probability that the brand A bulbs will have a mean lifetime which is at least 160 hours is 07972. The probability that the brand A bulbs will have a mean lifetime 250 hours more than the brand B bulbs is 0.0022.

5.True False. If random samples of size n are taken from a normally distributed population then the statistic 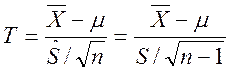has a Student's t distribution with n-1 degrees of freedom.

6.True False. Two samples of sizes 8 and 10 are drawn from two normally distributed populations with variances 20 and 30 respectively. The probability that the variance of the first sample is more than twice the variance of the second is 0.01<p<0.05.

7. True False An oil company produces unleaded petrol with mean lead content of 1% with a standard deviation of 0.02% (assume normal distribution). If 100 samples of 50 unleaded petrol samples each are obtained, the expected mean and standard deviation of the resulting sampling distribution of means if sampling were done a) with replacement b) without replacement, would be 1% + 0.0028 and 1% + 0.002. (Contributed by Douma Huub)

8. True False The confidence limits should be calculated using the standard deviation of the sampling distribution of means and not the population standard deviation. Thus for 95% we have Zc= 1.96 and for 99% we have Zc= 2.58. Thus for 95% the limits are:

`x + Zc(s/√n) = 2000 + 1.96(200/√1000) = 2000 + 12.4 m

For 99%

`x + Zc(s/√n) = 2000 + 2.58(200/√1000) = 2000 + 6.3 m

(Contributed by Douma Huub)

9. True False A sample poll of 250 constituents chosen at random from the entire voting district indicates that only 30 per cent were in favor of an industrial mineral mine being developed in the area. What is the 95% confidence limit for the proportion of all voters in favor of the mine development? And at a 97% confidence limit?

At a 95% confidence limit, 0.3 +/- 0.037

At a 97% confidence limit, 0.3 +/- 0.049

(Contributed by Joe Mazumdar)

10. True False An offshore drilling company has the choice of two drilling bits. Type I bits have a mean lifetime of 1200 hours with a standard deviation of 100 hours. Type II bits have a mean lifetime of 1400 hours with a standard deviation of 200 hours. If random samples of 125 of each bit are tested, what is the probability that the Type II bit will have a mean lifetime which is at least (i) 160 hours, (ii) 250 hours more than the type I bit? These probabilities are (i) .9772 (ii) .0062. (Contributed by Lawrence Gale)

11. True False We are studying the relationship between monthly earnings, and the individual's years of post secondary education. The first information we have from the sample collected are the sample mean and the sample variance. Monthly earnings: sample mean = a = 3,500, sample variance = s_a² = 12,100 => s_a = 110. Years of post secondary education: sample mean = b = 3.2, sample variance = s_b²= 7.5625=> s_b = 2.75

We want to know which sample is more dispersed. Since sample variance is the most common used measure of dispersion and s_x² > s_y², we can affirm that the sample of monthly earnings is more dispersed about the arithmetic mean. (Contributed by Alex Lombardia)